تابع پلهای - تابع هویساید
توابع پلهای:
تعریف : توابع پلهای، نوع خاصی از توابع هستند که شکل آنها مانند پلکان است. این تابع ها در بازههای مشخصی، تابع ثابت هستند.
معروفترین تابع پلهای، تابع جزء صحیح است یعنی تابع \([x]\). سادهترین آنها نیز تابع هِویساید (Heaviside) است که در ادامه به معرفی آن می پردازیم.
تعریف تابع هِویساید (Heaviside): ضابطه تابع هویساید به صورت زیر تعریف میشود:
\(u_c (t) = \left\{ \begin{array}{cc} 0 & t<c \\ 1 & t\geq c \end{array} \right. \)
همچنین نمودار تابع هویساید به صورت زیر است:
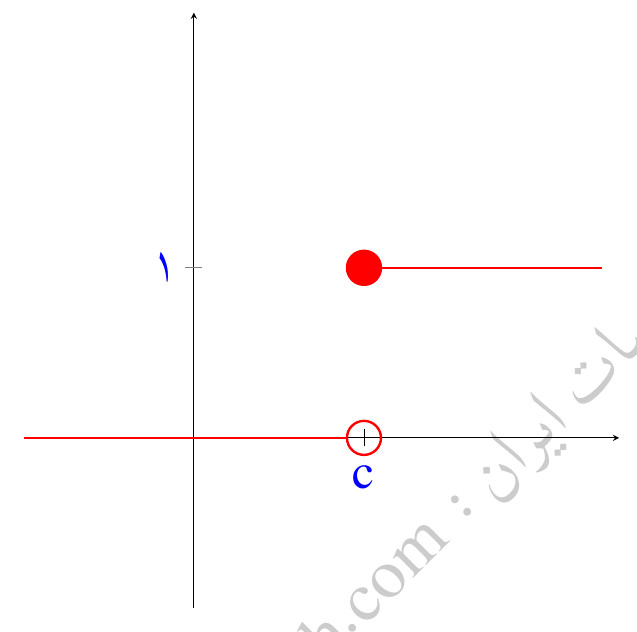
تابع هویساید معمولاً تابع پلهای نامیده میشود.
این تابع شکلهای متداول دیگری هم دارد:
\(u_c(t) = u(t-c) = H(t-c) = \left\{ \begin{array}{cc} 0 & t-c<0 \\ 1 & t-c\geq 0 \end{array} \right. \)
در این حالت اگر قرار دهیم \(t-c=x\) تابع هویساید به صورت زیر خلاصه میشود :
\( H(x) = \left\{ \begin{array}{cc} 0 & x<0 \\ 1 & x\geq 0 \end{array} \right. \)
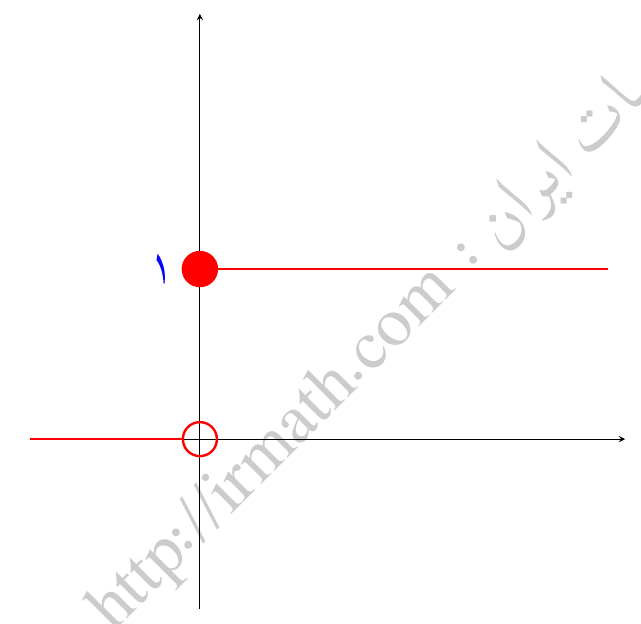
این تابع را میتوانیم مانند یک کلید ببینیم که برای زمان های کمتر از c خاموش است و مقدار صفر دارد و به محض رسیدن به زمان c، روشن شده و مقدار 1 میگیرد.
کمی فکر کنید ببینیم چگونه میتوانیم سایر اعداد مانند ۴- و ۷ را با این تابع بسازیم؟ تابع پلهای هویساید فقط میتواند اعداد یک و صفر را تولید کند، اما با استفاده از آن میتوانیم اعداد دیگری را بسازیم. به عنوان مثال تابع \( -4H(c) \) تابعی است که در اعداد کمتر از c مقدار صفر و در جاهای دیگر مقدار ۴- را میسازد. همچنین تابع \( 7H(c) \) در اعداد کمتر از c مقدار صفر و در جاهای دیگر مقدار ۷ را نتیجه میدهد.
اکنون فرض کنید میخواهیم تابعی داشته باشیم که ابتدا مقدار یک داشته باشد و از نقطه c به بعد مقدار آن صفر شود، یعنی برخلاف تابع هویساید عمل کند. این نیز ساده است، ببینید:
\( 1- H(c) = \left\{ \begin{array}{cc} 1-0 & c<0 \\ 1-1 & c\geq 0 \end{array} \right. = \left\{ \begin{array}{cc} 1 & c<0 \\ 0 & c\geq 0 \end{array} \right. \)
با حتی میتوانیم توابعی تعریف کنیم که ابتدا مقادیری به جز ۱ را در خروجی داشته باشند و از جایی به بعد صفر شوند، مثلاً تابع \( 3-3H(x) \) تا زمانی که \( x<c \) باشد مقدار ۳ را میدهد و سپس صفر میشود.
\( 3-3H(x-c) = 3-3 \left\{ \begin{array}{cc} 0 & x-c<0 \\ 1 & x-c\geq 0 \end{array} \right. = \left\{ \begin{array}{cc} 3 & x<c \\ 0 & x\geq c \end{array} \right. \)
در مثالهای زیر خواهیم آموخت که چگونه توابع چندضابطهای را با استفاده از تابع هویساید به صورت یک ضابطهای بنویسیم.
مثال ۱. تابع زیر را به صورت تابع هویساید تبدیل کنید:
\( f(x) = \left\{ \begin{array}{cc} 0 & x<6 \\ 25 & 6 \leq x < 8 \\ 0 & x \geq 8 \end{array} \right. \)
حل: ابتدا بیایید نگاهی به شکل این تابع داشته باشیم:
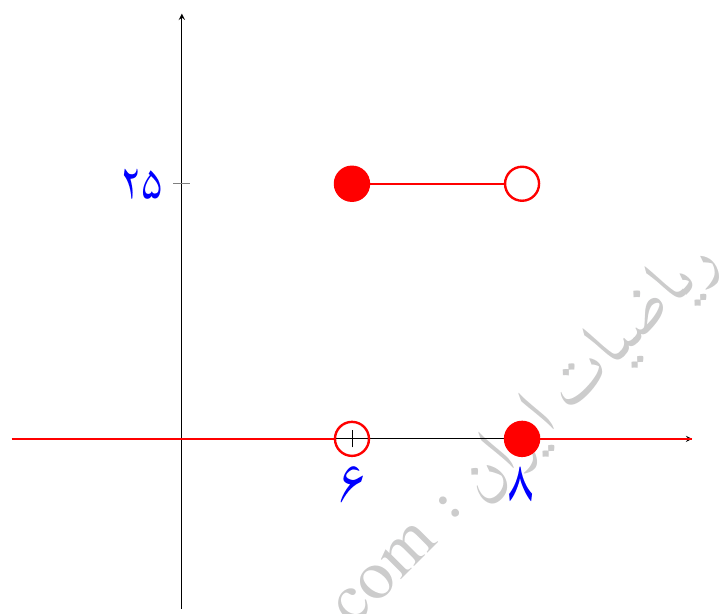
بازههای داده شده به ما این راهنمایی را میدهد که از \( H(6) \) و \(1-H(8) \) استفاده کنیم. داریم:
\( H(x-6) = \left\{ \begin{array}{cc} 0 & x<6 \\ 1 & x\geq 6 \end{array} \right. \)
\( 1- H(x-8) = \left\{ \begin{array}{cc} 1 & x<8 \\ 0 & x \geq 8 \end{array} \right. \)
اگر این دو تابع را با هم جمع کنیم، خواهیم داشت:
\( H(x-6) + 1 - H(x-8) = \left\{ \begin{array}{cc} 0 + 1 & x<6 \\ 1+1 & 6 \leq x < 8 \\ 1+0 & x \geq 8 \end{array} \right. = \left\{ \begin{array}{cc} 1 & x<6 \\ 2 & 6 \leq x < 8 \\ 1 & x \geq 8 \end{array} \right. \)
پس با کم کردن عدد ۱ از طرفین داریم:
\( H(x-6) - H(x-8) = \left\{ \begin{array}{cc} 0 & x<6 \\ 1 & 6 \leq x < 8 \\ 0 & x \geq 8 \end{array} \right. \)
و در نهایت با ضرب کردن طرفین مساوی در عدد ۲۵ به نتیجه مطلوب میرسیم. بنابراین :
\( \boxed{ f(x) = 25H(x-6) - 25H(x-8)} \)
مثال ۲. تابع زیر را به صورت تابع هویساید تبدیل کنید:
\( g(x) = \left\{ \begin{array}{cc} 0 & x<6 \\ 25 & 6 \leq x < 8 \\ 11 & x \geq 8 \end{array} \right. \)
حل:
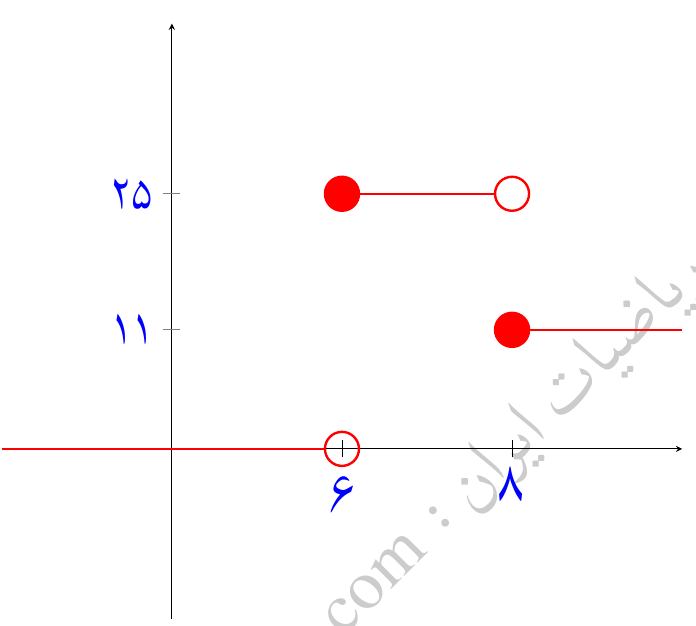
در این مثال بازههای داده شده به ما این راهنمایی را میدهد که از \( H(x-6) \) و \( H(x-8) \) استفاده کنیم. داریم:
\( H(x-6) = \left\{ \begin{array}{cc} 0 & x<6 \\ 1 & x\geq 6 \end{array} \right. \)
\( H(x-8) = \left\{ \begin{array}{cc} 0 & x<8 \\ 1 & x \geq 8 \end{array} \right. \)
اگر این دو تابع را با هم جمع کنیم، خواهیم داشت:
\( H(x-6) + H(x-8)= \left\{ \begin{array}{cc} 0 & x<6 \\ 1+0 & 6 \leq x < 8 \\ 1+1 & x \geq 8 \end{array} \right. \)
\( H(x-6) + H(x-8)= \left\{ \begin{array}{cc} 0 & x<6 \\ 1 & 6 \leq x < 8 \\ 2 & x \geq 8 \end{array} \right. \)
همانطور که می بینید، در بازه اول هر دو تابع صفر هستند و در بازه دوم فقط \( H(x-6) \) نقش ایفا میکند زیرا \( H(x-8) \) در این بازه صفر است. در بازه سوم، هر دو نقش دارند. اکنون باید ضرایب مناسب برای هر کدام را بیابیم. چون در بازه دوم فقط \( H(x-6) \) نقش دارد پس ضریب \( H(x-6) \) باید برابر با مقدار تابع در این بازه یعنی 25 باشد. پس با قرار دادن آن و قراردادن ضریب مجهول \( \alpha \) برای \( H(x-8) \)، با توجه به مقدار تابع در هر بازه ، ضریب مجهول \( \alpha \) را به دست می آوریم.
\( g(t) = 25 H(x-6) +\alpha H(x-8)= \left\{ \begin{array}{cc} 0+0 & x<6 \\ 25 + 0 \times \alpha & 6 \leq x < 8 \\ 25 +1 \times \alpha & x \geq 8 \end{array} \right. \)
\(= \left\{ \begin{array}{cc} 0 & x<6 \\ 25 & 6 \leq x < 8 \\ 25 + \alpha & x \geq 8 \end{array} \right.\)
که طبق ضابطه باید داشته باشیم :
\( 25 + \alpha = 11 \Longrightarrow \alpha = 11-25 = -14 \)
بنابراین
\( \boxed{ g(t) = 25 H(x-6) -14 H(x-8)} \)
مثال ۳. تابع زیر را به صورت تابع هویساید تبدیل کنید:
\( h(x) = \left\{ \begin{array}{cc} 3 & x<6 \\ 25 & 6 \leq x < 8 \\ 11 & x \geq 8 \end{array} \right. \)
حل:
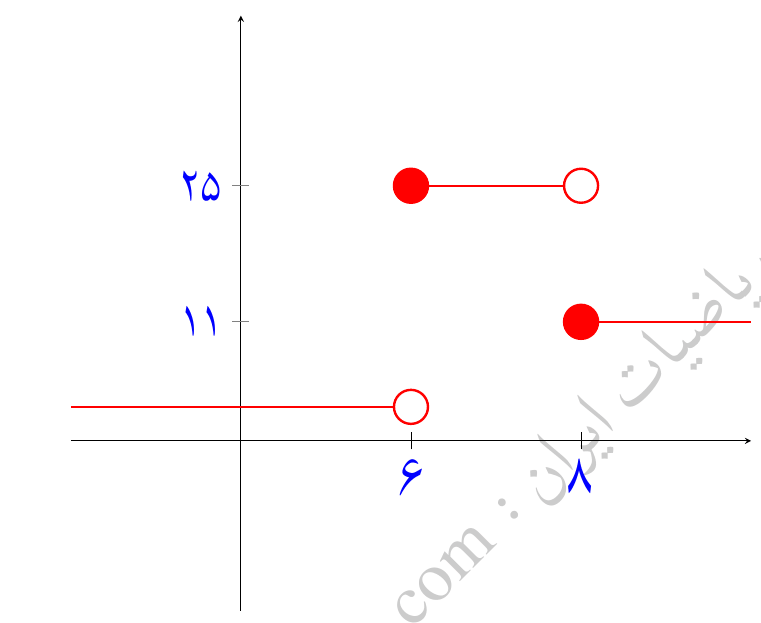
این مثال با مثال قبلی فقط در مقدار بازه اول تفاوت دارد. ببینیم این تفاوت چه تاثیری برفرمول نهایی تابع هویساید خواهد گذاشت. در این مثال نیز از توابع \( H(x-6) \) و \( H(x-8) \) استفاده میکنیم. اگر از تابع مقدار ۳ را کم کنیم خواهیم داشت:
\( h(x) - 3 = \left\{ \begin{array}{cc} 0 & x<6 \\ 22 & 6 \leq x < 8 \\ 8 & x \geq 8 \end{array} \right. \)
این تابع دقیقاً شبیه مثال قبل شد، پس با کمی محاسبات خواهیم داشت:
\( h(t) -3 = 22 H(x-6) -14 H(x-8) \Longrightarrow \)
\( \boxed{ h(t) = 3+ 22 H(x-6) -14 H(x-8) } \)
تمرین : آیا میتوانید تابع زیر را به صورت توابع هویساید تبدیل کنید؟
\( f(x) = \left\{ \begin{array}{cc} -4 & x<6 \\ 25 & 6 \leq x < 8 \\ 16 & 8 \leq x < 30 \\ 10 & x \geq 30 \end{array} \right. \)
در درس های بعد خواهید دید که چگونه از این تابع در معادلات دیفرانسیل استفاده خواهیم کرد.

