ارتباط بین جواب‌های معادله‌ی همگن و ناهمگن نظیر

[tabs] [tab_item title="قضیه اول"]

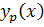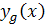قضيه 1.3: اگر يک جواب خصوصي معادله ي خطي استاندارد ناهمگن مرتبه دوم و جواب عمومي معادله ي همگن نظيرش باشد آنگاه

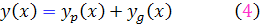
جواب عمومي معادله خطي استاندارد ناهمگن مرتبه دوم است.

[/tab_item] [tab_item title="اثبات " ]

اثبات: با توجه به مفروضات قضيه، 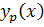يک جواب خصوصي معادله ي در تعريف 3.2 و 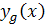جواب عمومي معادله ي در تعريف 3.4 مي باشند. ابتدا نشان مي دهيم معادله ي يک جواب معادله ي است و سپس نشان مي دهيم که اين جواب، جواب عمومي نيز هست يعني هر جواب ديگر معادله را مي توان از به دست آورد.

براي آنکه نشان دهيم يک جواب است، تابع و مشتقاتش را در معادله قرار مي دهيم. داريم :

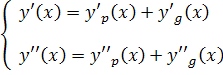
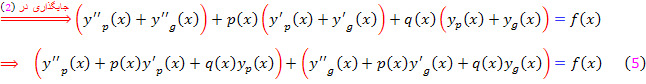
اما چون 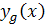جواب عمومي معادله است پس در آن صدق مي کند يعني

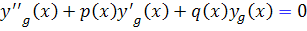
بنابراين از نتيجه مي شود :

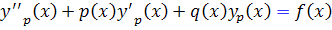
اين نيز برقرار است زيرا 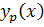يک جواب خصوصي براي معادله است. بنابراين در صدق مي کند و يک جواب آن است.

براي آنکه نشان دهيم جواب عمومي معادله است، فرض کنيد 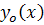جواب ديگري از معادله باشد. اگر 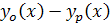را در معادله ي قرار دهيم خواهيم داشت :

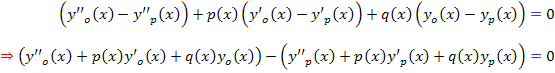
اما مقدار هريک از پرانتز هاي سمت چپ برابر با 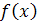است. ازبرقراري اين تساوي نتيجه مي شود که 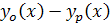جوابي از معادله ي است.

اما 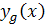جواب عمومي معادله بود، بنابراين هر جواب ديگر معادله ، از جمله 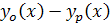را مي توان به ازاي ثابت هايي مانند 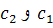از جواب عمومي به دست آورد. بنابراين

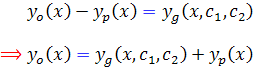
يعني نشان داديم که هر جواب ديگر از معادله را مي توانيم از معادله ي 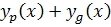به دست آوريم. پس 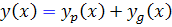جواب عمومي معادله ي است.

[/tab_item] [tab_item title="قضیه دوم"]

این قضيه نشان مي دهد که اگر دو جواب از معادله همگن را بدانيم، آنگاه هر ترکيب خطي ازآن ها، جواب ديگري براي معادله ي همگن به دست مي دهد، که مي تواند راهنماي ما در به دست آوردن جواب عمومي معادله باشد. در آينده شرايطي را بيان خواهيم کرد که با استفاده از اين قضيه با آن شرايط ، جواب عمومي معادله همگن را به دست آوريم.

قضيه 2.3: اگر 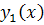و 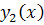دو جواب براي معادله همگن باشند، آنگاه براي هر مقدار حقيقي ِ 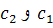، تابع 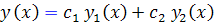نيز يک جواب براي معادله همگن است.

[/tab_item] [tab_item title="اثبات"]

اثبات: براي اثبات کافي است نشان دهيم 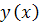در معادله همگن صدق مي کند :

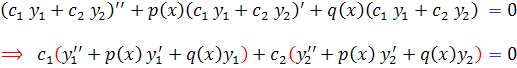
اما فرض مسأله بيان مي کند که تساوي بالا درست است چرا که هر يک حاصل از پرانتزها برابر با صفر است ، زيرا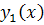 و 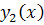جواب هاي معادله ي همگن هستند. بنابراين 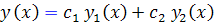در صدق مي کند. پس جواب معادله همگن است.

[/tab_item] [/tabs]