پایان ترم مبانی ریاضیات دکتر خشایارمنش ترم اول 84-1385 فردوسی مشهد

اللهم صل علی محمد و آل محمد

1. الف: نشان دهید نقاط با مختصات گویا واقع بر دوایر به مرکز مبدأ مختصات و شعاع های گویا، شمارای نامتناهی است .

ب: فرض کنید X مجموعه ی نقاط قسمت (الف) باشد. رابطه را روی X به گونه ای تعریف کنید که خوش ترتیب باشد .

2. نشان دهید

3. قضیه ی کانتور را برای اعداد کاردینال بیان و اثبات کنید.

4. اصل انتخاب را بیان کنید و نشان دهید اگر تابعی برو باشد آنگاه زیر مجموعه ی C از A هست که B ~ C .

5. فرض کنید H یک مجموعه ی دلخواه و ناتهی باشد و فرض کنید مجموعه ی تمام زیر مجموعه های خوش ترتیب از H مانند باشد.

الف: رابطه ی 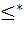را روی چنان تعریف کنید که مرتب جزئی باشد.

ب: فرض کنید می دانیم در قسمت الف در شرایط لم زورن صدق می کند. نشان دهید H خوش ترتیب است.

6. به کمک اصول پئانو در اعداد طبیعی نشان دهید برای هر سه عدد طبیعی x و y و z داریم :