معادله دیفرانسیل همگن
براي اينکه بدانيم معادلات ديفرانسيل همگن چه معادله ايست، ابتدا بايستي توابع همگن را بشناسيم و با برخي از ويژگي هاي آن آشنا شويم. در اين درس ابتدا به معرفي تابع همگن مي پردازيم و سپس معادله همگن را تعريف کرده و به چگونگي حل آن ها مي پردازيم.
تعريف تابع همگن:
تابع 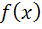 را تابع همگن ِ مرتبه ي n گوييم هرگاه براي هر t، داشته باشيم
را تابع همگن ِ مرتبه ي n گوييم هرگاه براي هر t، داشته باشيم
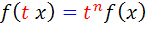
البته بايد به خاطر داشته باشيم که تابع f ، در نقاط x و tx ، تعريف شده باشد.
تابع 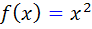 نمونه اي از تابع همگن مرتبه 2 است زيرا براي هر tx ، t در دامنه ي f است و داريم :
نمونه اي از تابع همگن مرتبه 2 است زيرا براي هر tx ، t در دامنه ي f است و داريم :
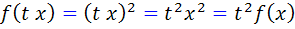
تابع همگن براي توابع چند متغيره نيز تعريف مي شود. چون در اين درس، بيشتر با توابع دو متغيره سر و کار داريم ، تعريف تابع همگن دو متغيره را نيز بيان مي کنيم.
تعريف تابع همگن دو متغيره:
تابع 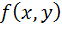 را تابع همگن ِ مرتبه ي n گوييم هرگاه براي هر t داشته باشيم
را تابع همگن ِ مرتبه ي n گوييم هرگاه براي هر t داشته باشيم
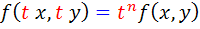
به شرط اينکه نقاط 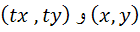 در دامنه ي تابع باشند.
در دامنه ي تابع باشند.
[/tab_item] [tab_item title="ویژگیهای تابع همگن"]
ويژگي هاي تابع همگن:
اگر توابع 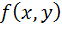 و
و 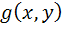 ، همگن مرتبه ي n باشند، آنگاه توابع
، همگن مرتبه ي n باشند، آنگاه توابع 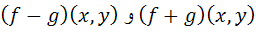 همگن مرتبه ي n و تابع
همگن مرتبه ي n و تابع 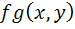 همگن مرتبه ي 2n و تابع
همگن مرتبه ي 2n و تابع 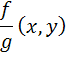 ، با شرط
، با شرط 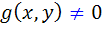 ، همگن مرتبه ي صفر است.
، همگن مرتبه ي صفر است.
اثبات اين ويژگي ها ساده است و تنها با بکار بردن تعريف به دست مي آيد. براي نمونه نشان مي دهيم که تابع خارج قسمت، همگن مرتبه ي صفر است.
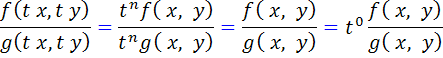
اکنون آمادگي پذيرش مفهوم معادله ديفرانسيل ِ همگن هستيم :
[/tab_item] [tab_item title="معادله دیفرانسیل همگن"]
تعريف معادله ديفرانسيل همگن:
اگر توابع 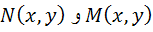 ، در معادله ديفرانسيل مرتبه اول ِ
، در معادله ديفرانسيل مرتبه اول ِ
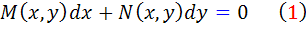
توابعي همگن ِ همدرجه ، مثلا ً از درجه ي n باشند، آنگاه گوييم معادله 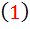 معادله ديفرانسيل همگن مرتبه ي n است.
معادله ديفرانسيل همگن مرتبه ي n است.
اين تعريف همسنگ تعريف زير است :
معادله ي
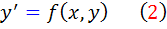
يک معادله ديفرانسيل همگن است اگر تابع 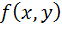 ، همگن از درجه ي صفر باشد.
، همگن از درجه ي صفر باشد.
نکته 2.2: هر تابع ثابت، يک تابع همگن از مرتبه ي صفر است ولي عکس آن درست نيست. يعني توابع همگن مرتبه ي صفر ، لزوما ً ثابت نيستند. براي نمونه تابع
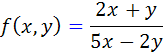
همگن مرتبه ي صفر است که ثابت نيست.
[/tab_item] [tab_item title="روش حل معادله همگن"]
چگونگي حل معادله همگن:
معادلات همگن ، با يک تغيير متغير مناسب ، به معادلات جداپذير تبديل مي شوند. پس مي توانستيم اين معادلات را در دسته ي معادلات جداپذير شدني قرار دهيم؛ اما چون معادلات همگن شکل ونام ويژه اي دارند و حتي دسته اي از معادلات همگن شدني هستند، آن ها را جداگانه بررسي مي کنيم.
معادله همگن 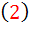 را در نظر بگيريد. به ياد داريم که تابع
را در نظر بگيريد. به ياد داريم که تابع 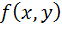 ، همگن از مرتبه ي صفر است. پس براي هر t داريم :
، همگن از مرتبه ي صفر است. پس براي هر t داريم :
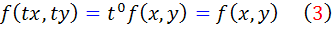
اکنون اگر به t مقدار ويژه ي  را نسبت دهيم ، يعني قراردهيم
را نسبت دهيم ، يعني قراردهيم 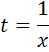 ، معادله ي
، معادله ي 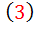 به صورت زير تبديل مي شود:
به صورت زير تبديل مي شود:
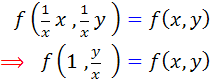
اکنون تغيير متغير 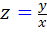 را انتخاب مي کنيم. داريم :
را انتخاب مي کنيم. داريم :
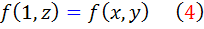
و همچنين
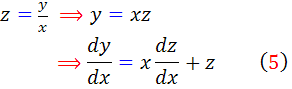
اکنون در رابطه ي  ، از رابطه هاي
، از رابطه هاي  و
و  مقدار مي گذاريم :
مقدار مي گذاريم :
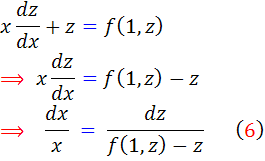
که معادله ي 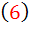 ، يک معادله جداپذير استاندارد بر حسب x و z است که در قسمت هاي قبل چگونگي حل آن را آموختيم. پس از حل
، يک معادله جداپذير استاندارد بر حسب x و z است که در قسمت هاي قبل چگونگي حل آن را آموختيم. پس از حل 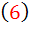 به جاي z ، مقدار آن يعني
به جاي z ، مقدار آن يعني  را قرار مي دهيم و معادله حاصل را مرتب مي کنيم.
را قرار مي دهيم و معادله حاصل را مرتب مي کنيم.
به مثال زير توجه کنيد.
[/tab_item] [tab_item title="مثال"]مثال 9.2: ابتدا نشان دهيد معادله ي 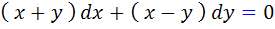 يک معادله همگن است و سپس جواب عمومي آن را بيابيد.
يک معادله همگن است و سپس جواب عمومي آن را بيابيد.
حل: در اين مثال 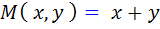 و
و 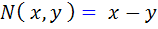 هر دو ، توابعي همگن مرتبه ي اول هستند، پس معادله داده شده همگن است.
هر دو ، توابعي همگن مرتبه ي اول هستند، پس معادله داده شده همگن است.
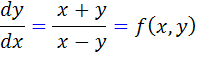
با قرار دادن 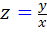 داريم:
داريم:
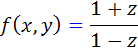
و y = z x ، پس:
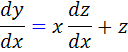
بنابراين:
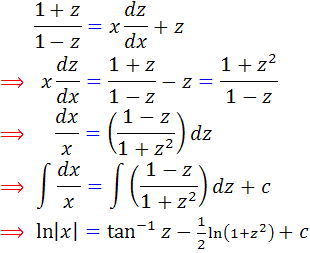
اکنون قرار مي دهيم 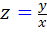 :
:
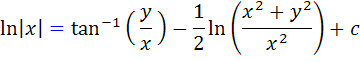
که اين جواب عمومي معادله داده شده است.
[/tab_item] [/tabs]
- بازدید: 35874

- کاربران 818
- مطالب 1059
- نمایش تعداد مطالب 16192205