حاصلضرب دكارتی

حاصلضرب دکارتی

[tabs ] [tab_item title="تعریف" ]

حاصلضرب دكارتي مجموعه‌ها:

تعریف:اگر A و B دو مجموعه باشند، «حاصلضرب دكارتي» آن‌ها را با نماد «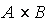 » نمايش مي‌دهيم و به صورت زير تعريف مي‌كنيم:

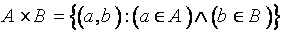
بنابراين حاصلضرب دكارتي دو مجموعه، يك مجموعه است و اعضاي آن دوتايی‌هاي مرتب ( زوج هاي مرتب ) هستند. در هر دوتايي مرتب، مؤلفه‌ي اول ( a ) از مجموعه‌ي اول ( A ) و مولفه‌ي دوم ( b ) از مجموعه‌ي دوم ( B ) انتخاب مي‌شود.

[/tab_item] [tab_item title="مثال"]

مثال:

مثال: اگر 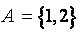و 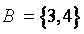در اين صورت

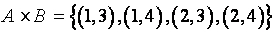
همچنين

[/tab_item] [tab_item title="نکته"]

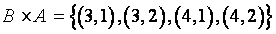
حاصلضرب دکارتی جابجایی نیست:

مثال قبل نشان مي‌دهد كه

حاصلضرب دكارتي مجموعه‌ها، جابجايي نست.

يعني در حالت كلي «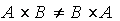 »، زيرا اگر A و B مجموعه‌هاي ناتهي و مجزا باشند، عضوي مانند x در A ‌هست كه در B نيست. پس 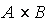داراي دوتايي مرتبی با مولفه‌ي اول x است. اما 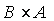چنين دوتايي مرتبی ندارد.

 

[/tab_item] [tab_item title="تعمیم"]

گسترش (تعميم) حاصلضرب دكارتي:

حاصلضرب دكارتي مجموعه‌ها را مي‌توان به بيش از دو مجموعه گسترش داد. حاصلضرب دكارتي n مجموعه ي 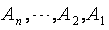به صورت زير تعريف مي‌شود:

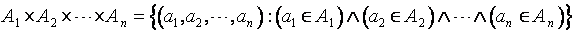
درواقع حاصلضرب دكارتي n مجموعه، مجموعه‌ي n-تايیهای مرتبی است كه هر n-تایی مرتب، مؤلفه اول خود را از مجموعه اول و مؤلفه دوم خود را از مجموعه دوم و ... و مؤلفه n-ام خود را از مجموعه ي n-ام می‌گيرد.

[/tab_item][/tabs]