معادلات جداپذیر شدنی : دسته دوم
رای دهی: 5 / 5
معادلات ديفرانسيل جداپذير شدني - دسته دوم: معادله ي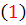 
را مي توان به صورت کلي تر زير نوشت:
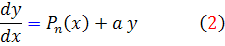
که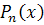 
، يک چندجمله اي از x از درجه ي n است.
براي تبديل اين گونه معادلات به معادلات جداپذير، بايست n بار تغيير متغير بگيريم. با مثال زير اين روش را شرح مي دهيم. در اين مثال براي سادگي، چندجمله اي را از درجه ي 2 انتخاب کرده ايم .
مثال 5.2: جواب عمومي معادله ديفرانسيل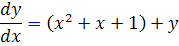 
را بيابيد.
حل: ابتدا تغيير متغير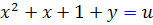 
را انتخاب مي کنيم و از آن نسبت به x مشتق مي گيريم:
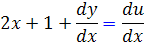
اما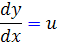 
. پس
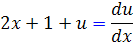
اکنون در اين معادله جديد، تغيير متغير 2x + 1 + u = v را انتخاب مي کنيم و از آن نسبت به x مشتق مي گيريم :
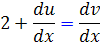
اما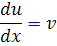 
. پس
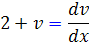
که اين يک معادله ديفرانسيل جداپذير است و جواب عمومي آن به سادگي محاسبه مي شود:
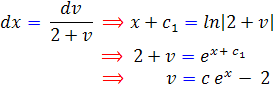
که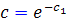 
. اکنون مقدار v را قرار مي دهيم، داريم:
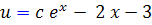
و با قرار دادن مقدار u ، تابع y به دست مي آيد:
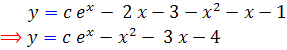
که اين معادله، جواب عمومي معادله ديفرانسيل داده شده است. امتحان کنيد !
.
نکته 1.2: در معادله ي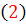 
، به جاي 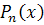مي توان توابعي از x که مشتق مرتبه ي n ام آن عدد ثابتي باشد، قرار داد. در اين صورت نيز با n بار تغيير متغير گيري و انجام روش ياد شده، به جواب عمومي معادله مي رسيم.
