29.1. اعداد گنگ و اعداد گویا
رای دهی: 5 / 5
به نام خدا
الهم صل علی محمد و آل محمد
اينکه مي گوييم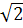 
عددي گنگ است يعني چه ؟ آيا به اين معني است که 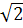قادر به صحبت نيست ؟ !!! مسلما ً اين گونه نيست. در رياضيات به اعدادي که گويا نباشند، اعداد گنگ ( اصم ) مي گويند.
اعداد گويا چه نوع اعدادي هستند؟ آيا اين اعداد نيز اعداد « سخن گو » هستند؟ خير ؛ به عددي که بتوان آن را با يک کسر معمولي بيان کنيم ، يک « عدد گويا » مي گوييم.
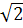عددي گنگ است زيرا هيچ کسري به صورت 
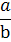وجود ندارد که برابر با 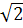باشد. اگر 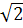را محاسبه کنيم خواهيم داشت :
( در پايان اين قسمت اثبات خواهيم کرد که 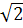عددي گنگ است. )
دقت کنيد که در ارقام ِ 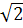هيچ الگويي وجود ندارد و هيچ گروهي از ارقامش تکرار نمي شوند.
بنابراين اين سوال پيش مي آيد که آيا همه ي اعداد گويا ، در نمايش اعشاري ، يک گروه از ارقامشان دوره اي هستند و تکرار مي شوند؟
براي مشخص شدن مطلب ، اجازه دهيد چند کسر را ارزيابي کنيم :
که اين عدد را مي توان به صورت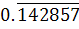 
نوشت. که داراي يک گروه شش رقمي تکراري است يا به عبارتي دوره ي گردش ِ 
، شش رقمي است و آن ارقامي که بالاي آن ها خط کشيده ايم از ابتداي خط تا انتهاي آن به ترتيب تکرار مي شوند.
اما مقدار کسر ِ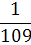 
را ببينيد :
چنانچه ملاحظه نموديد ما اين کسر را تا بيش از 100 رقم اعشار محاسبه نموديم اما هيچ دوره ي گردشي مشاهده نمي کنيم. آيا مي توانيم نتيجه بگيريم که 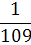عددي گنگ است ؟ اگر چنين باشد که تعريف قبلي ما براي اعداد گنگ باطل مي شود !!!...
آيا اگر مقدار 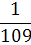را کمي بيشتر محاسبه کنيم، اتفاق خاصي نخواهد افتاد؟ ببينيم اگر 10 رقم اعشار جلوتر رويم چه مي شود :
به نظر مي رسد يک الگوي تکراري شروع شود و آغاز آن 0091 باشد. محاسبات را بيشتر مي کنيم( بيش از 200 رقم ) ، آيا حدس ما درست خواهد بود ؟ ببينيد :
اگر محاسبات را تا 332 رقم اعشار ادامه دهيم ، الگو واضح خواهد شد :
پس مي توانيم اين محاسبات را متوقف کنيم و نتيجه بگيريم ( البته بدون اثبات) که « نمايش يک کسر معمولي به صورت عدد اعشاري ، همواره يک دوره ارقام چرخشي دارد. » البته بعضي از اين کسر ها در اين نمايش، دوره ي چرخش کوتاهي دارند : مثلا ً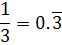 
دوره ي چرخش يک رقمييا 
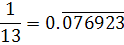يک دوره ي چرخشي 6 رقمي دارد و بعضي ها مانند 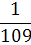که دوره ي 108 رقمي دارد، دوره ي طولاني تري دارند.
اين ، گواهي بر آن است که يک کسر داراي نمايش ِ اعشاري متناوب است ولي اعداد گنگ چنين نيستند.
اکنون ثابت مي کنيم که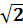 
را نمي توان به صورت يک کسر نوشت که آن نتيجه خواهد داد 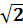عددي گنگ است.
... « فرض کنيم 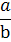کسري با کوچکترين جملات است که در آن a و b هيچ مقسوم عليه مشترکي ندارند. فرض کنيم 
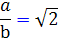. دو طرف تساوي را به توان 2 مي رسانيم : 
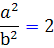بنابراين 
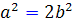. يعني 
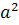عددي زوج است . چونتوان دوم هر عدد فرد، عددي فرد است پس چون 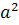زوج است ، a نمي تواند عددي فرد باشد ؛ پس a زوج است و مي توان فرض کرد a = 2k . بنابراين 
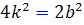که نشان مي دهد 
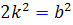. پس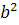 
زوج است و b نيز زوج خواهد شد. پس در کل از اينکه 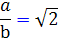باشد ، به اين نتيجه رسيديم که a و b بايستي اعداد زوجي باشند که در اين صورت a و b داراي حداقل يک مقسوم عليه مشترک ( يعني 2 ) هستند که اين نتيجه با فرض اوليه ي ما ( a و b هيچ مقسوم عليه مشترکي ندارند ) در تناقض است. بنابراين فرض اينکه 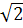را بتوان به صورت يک کسر نوشت باطل است يعني 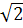عددي گنگ است . » ... .
شايد اين اثبات براي شما اصرار آميز و گيج کننده باشد اما با کمي دقت و پيگيري ِ گام به گام ِ آن ، به زيبايي اين اثبات پي خواهيد برد.
