30.1. مجموع اعداد متوالی
رای دهی: 4 / 5
آيا مي دانيد چه اعدادي را مي توانيم به صورت مجموع اعداد ِ طبيعي متوالي بنويسيم ؟
اگر نمي دانيد اين مطلب را پي گيريد تا ببينيد چه اعدادي را مي توانيم به صورت مجموع اعداد طبيعي متوالي بنويسيم.
از عدد 2 تا 40 شروع مي کنيم و سعي خواهيم کرد براي هر کدام ، ليستي از اعداد ِ متوالي بيابيم که مجموع آن ها با عدد انتخاب شده برابر باشد.
نکته 1 : نمايش اعداد به صورت مجموع ِ اعدادِ متوالي ، يکتا نيست ؛ مثلا" 30 را به صورت هاي زير مي توان نمايش داد:
9+8+7+6=11+10+9=30
نکته 2 : يک بازرسي در اعداد بالا نشان مي دهد : اعدادي را که به صورت تواني از 2 هستند، نمي توانيم به صورت مجموع اعداد متوالي بنويسيم . ( در پايان اين قسمت ، اين مطلب را اثبات مي کنيم. )
نکته ي 2 حقيقت ِ جالبي است که توقع نمي رفت چنين باشد. همچنين با ساختن يک چنين ليستي از اعداد به صورت مجموع ِ اعداد ِ متوالي ، الگوهايي را مشاهده خواهيم کرد. يکي از اين الگوهاي واضح در مورد اعداد مثلثي است. n - مين عدد مثلثي ، مجموع n عدد ِ طبيعي نخست متوالي است. مثلا ً
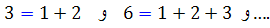
يا اين که n - مين مضرب از عدد 3 را که 3n مي ناميم، همواره مي توانيم به صورت مجموع ِِ n -مين عدد طبيعي و اعداد قبل و بعدش نمايش دهيم. يعني
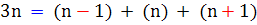
با کمي دقت شما نيز مي توانيد چنين الگو هايي را کشف کنيد؛ زيرا که ديدن الگوهاي اعداد و روابط بين آن ها يکي از جالب ترين بخش هاست.
اکنون ثابت مي کنيم يک عدد را کِي مي توانيم به صورت مجموع ِحداقلِ ِ دو عدد طبيعي و متوالي بنويسيم:
اگر a وb دو عدد طبيعي باشند که b ازa بزرگتر است ، مجموع عددهاي طبيعي متوالي بينa و b چه مقاديري مي توانند باشند؟
با استفاده از فرمولِِِِ مجموع ِ يک سري عددي مي توان اين مقدار را به دست آورد ؛ که اين مقدار برابر است با نصف حاصلضرب مجموع کران بالا و کران پايين در تعداد جملات.
بنابر ايناگر مجموع اعداد طبيعي متوالي بين a وb راS بناميم ، از فرمول زير به دست مي آيد :
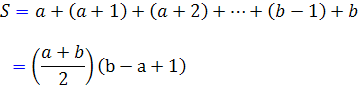
که در اين حالت ، a جمله ي پاييني و b جمله ي بالايي و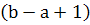 
تعداد جملات بين a و bاست. ( ممکن است اين سوء تفاهم پيش آيد که با استفاده از قوانين جمع ، مي توانيم پرانتزهاي بين اعداد در فرمول بالا را حذف کنيم. با حذف اين پرانتزها اعداد -1 و +1 و ... با هم ساده مي شوند و تنها تعدادي a و تعدادي b باقي مي ماند. براي جلوگيري از اين گونه موارد بيان مي کنيم که منظور از 
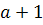، عدد طبيعي ِ بعد از a است و منظور از 
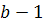نيز عدد طبيعي قبل از b است و ... . ممکن است در مکاني مثلا ً 
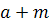و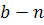 
با هم برابر شوند ( m وn عدد طبيعي هستند )، که در اين حالت نيز تنها يکي از آن ها را وارد مي کنيم.پس در حالت کلي منظور از مجموع بالا ، مجموع اعداد طبيعي بينa وb با احتساب خودa وb است و اين اعداد بدون تکرار در نظر گرفته مي شوند. ) .
پس
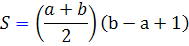
دو طرف تساوي را دو برابر مي کنيم :
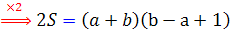
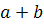را x مي ناميم و 
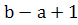را y . چون a و b اعداد طبيعي هستند و 
، x و y نيز اعداد طبيعي اند. از آنجا که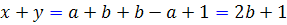 
عددي فرد است ، بنابراين يکي از x وyفرد است و ديگري زوج . ( دقت داريم که فقط مجموع ِ يک عدد فرد و يک عدد زوج ، عددي فرد است. )
اکنون تساوي 2S = xy و وضعيت هاي x و y ، دو حالت زير را پيش روي ما قرار مي دهد :
حالت اول :S تواني از 2 است :
فرض مي کنيم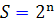 
. بنا بر اين 
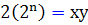يا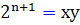 
. تنها حالتي ، که يک توان از 2 را مي توانيم به صورت حاصلضرب يک عدد فرد در يک عدد زوج بنويسيم ، حالتي است که عدد فرد ، عدد 1 باشد. اگر x=1 باشد ، يعني :
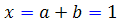
، در اين صورت a , b نمي توانند اعداد طبيعي باشند ، زيرا مجموع هيچ دو عدد طبيعي ، برابر با 1 نيست.
و اگر y برابر با 1 باشد ، يعني :
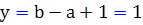
، پس بايد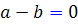 
يا به عبارتي a و b با هم برابر باشند که اين نيز اتفاق نمي افتد.
بنابراين در اين حالت نمي توانيمS را به صورت مجموع ِ اعداد ِ متوالي بنويسيم.
حالت دوم :S تواني از 2 نيست :
فرض مي کنيم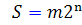 
که m عدد فردي بزرگتر از 1 است. در اين صورت 
.
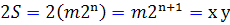در اين حالت مي توانيم اعداد طبيعي a و bرا طوري بيابيم که 
باشد و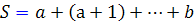 
.
دقت داريم که دو عدد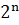 
و m برابر نيستند زيرا m فرد است و 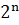زوج .بنابراين يکي از آنها بزرگتر از ديگري است. فرض کنيم x آن عدد ِ بزرگتر و y آن عدد ِ کوچکتر باشد. با اين انتخاب جواب ِ a و b مشخص مي شود زيرا از رابطه ي 
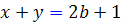مقدار b مشخص مي شود 
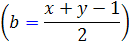و از رابطه ي 
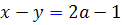مقدار a مشخص مي شود 
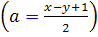. همچنين 
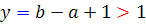و بنابر اين .
بنابراين ، آن عدد طبيعي را مي توانيم با مجموع ِ اعداد ِ طبيعي متوالي نمايش دهيم که تواني از 2 نباشد.
با اين مطلب به پايان فصل اول در شگفتي ها و زيبايي هاي رياضيات مي رسيم.
