روش حل معادله دیفرانسیل خطی مرتبه اول
- مقطع تحصیلی: کارشناسی
به نام خدا
الهم صل علی محمد و آل محمد
اگر روش حل معادلات کامل را به ياد داشته باشيد، روش حل معادلات خطي براي شما آسان خواهد بود. توجه کنيد :
معادله خطي  را در نظر مي گيريم و آن را به صورت ديفرانسيلي مي نويسيم :
را در نظر مي گيريم و آن را به صورت ديفرانسيلي مي نويسيم :
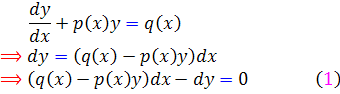
اکنون براي حل معادله ي  ، از معادلات کامل کمک مي گيريم. دقت داريم که معادله ي
، از معادلات کامل کمک مي گيريم. دقت داريم که معادله ي  کامل نيست و
کامل نيست و
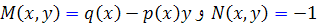
اما
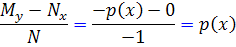
، تابعي از x است. با استفاده از حالت اول ِ تعيين عامل انتگرال ساز ، معادله داراي عامل انتگرال سازي به صورت زير است :
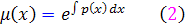
بنابراين اگر عامل انتگرال ساز  را در معادله ي
را در معادله ي  ضرب کنيم ، يک معادله ي کامل به دست مي آيد که قبلا ً روش حل آن را آموختيم. اکنون به حل آن مي پردازيم و يک فرمول کلي به دست مي آوريم تا يک بار براي هميشه از روش معادلات کامل استفاده کرده باشيم و در مثال ها از اين فرمول استفاده مي کنيم.
ضرب کنيم ، يک معادله ي کامل به دست مي آيد که قبلا ً روش حل آن را آموختيم. اکنون به حل آن مي پردازيم و يک فرمول کلي به دست مي آوريم تا يک بار براي هميشه از روش معادلات کامل استفاده کرده باشيم و در مثال ها از اين فرمول استفاده مي کنيم.
پس :
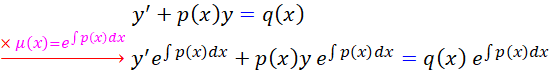
اما اگر کمي دقت کنيم متوجه مي شويم که طرف چپ تساوي بالا را مي توانيم اين گونه بنويسيم :
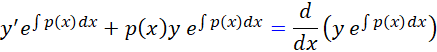
بنابراين خواهيم داشت :
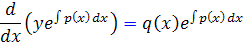
که با انتگرال گيري نسبت به x جواب عمومي به دست مي آيد :
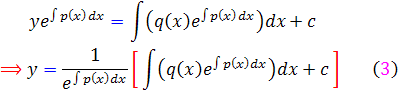
و اگر قرار دهيم 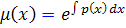 ، فرمول ساده تر زير به دست مي آيد که جواب عمومي معادله خطي مرتبه اول از ان حاصل مي شود :
، فرمول ساده تر زير به دست مي آيد که جواب عمومي معادله خطي مرتبه اول از ان حاصل مي شود :
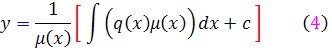
اين فرمول را به خاطر بسپاريد !!!
ديديم که در حل معادلات خطي ، آن ها را به معادلات کامل تبديل کرديم و با استفاده از روش حل معادلات کامل آن ها را حل کرديم. ممکن است سؤال شود که چرا معادلات خطي را جزء معادلات کامل شدني قرار نداديم؟
در پاسخ بايد بگوييم : درست است که معادلات خطي ، با استفاده از معادلات کامل حل مي شوند ؛ اما دو عامل باعث مي شود آن ها را از معادلات کامل جدا کنيم : يکي اينکه معادلات خطي شکل خاصي دارند و رده ي بزرگي از معادلات ديفرانسيل را شامل مي شوند و ديگر اينکه بسياري از معادلات ديفرانسيل را مي توان به معادلات خطي تبديل کردکه آن ها را در بخش هاي آينده بررسي خواهيم کرد.
قبل از آنکه وارد بخش معادلات کامل شدني شويم، به جاست چند مثال در معادلات خطي حل کنيم .
مثال زير از ميان تست هاي کنکور کارشناسي ارشد مهندسي معدن گرايش استخراج سال 1380 انتخاب شده است :
مثال 18.2: جواب عمومي معادله ديفرانسيل 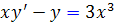 برابر است با:
برابر است با:
1. 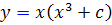
2. 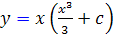
3. 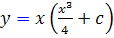
4. 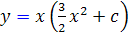
حل : ابتدا معادله را به شکل استاندارد ِ خطي مي نويسيم :
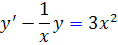
بنابراين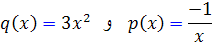 . پس عامل انتگرال ساز به صورت زير است :
. پس عامل انتگرال ساز به صورت زير است :
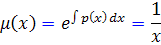
اکنون جواب عمومي را از فرمول  محاسبه مي کنيم:
محاسبه مي کنيم:
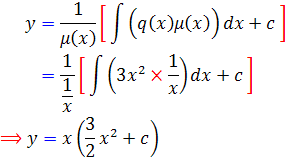
بنابراين گزينه ي 4 پاسخ صحيح مي باشد.
مثال زير نيز از تست هاي کنکور کارشناسي ارشد مهندسي معدن سال 1380 انتخاب شده است :
مثال 19.2: جواب عمومي معادله ديفرانسيل 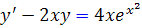 برابر است با :
برابر است با :
1. 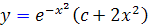
2. 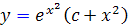
3. 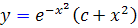
4. 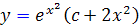
حل: در اين مثال داريم:
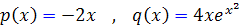
و عامل انتگرال ساز اين گونه است :
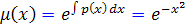
بنابراين با استفاده از فرمول  ، جواب عمومي زير حاصل مي شود :
، جواب عمومي زير حاصل مي شود :
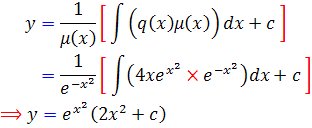
بنابراين پاسخ صحيح ، گزينه ي 4 خواهد بود.
















