پاسخ تمرین هایی در معادلات دیفرانسیل
جناب آقاي ياشار سعيدي، دانشجوي رشته ي مهندسي مکانيک ، ورودي 85 از دانشگاه آزاد اسلامي تبريز ، اين پاسخ ها را به شما و تمامي بازديدکنندگان محترم سايت تقديم مي کنيم :
پاسخ ها :
1. براي به دست آوردن معادله ديفرانسيل اين منحني ها، به تعداد ثابت ها، از معادله داده شده مشتق مي گيريم و با استفاده از تابع و مشتقاتش ، ضرايب ثابت را حذف مي کنيم و رابطه ي بين تابع و مشتقاتش را به دست مي آوريم :
الف :
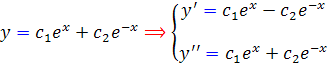
با توجه به معادله ي y و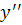 
، در مي يابيم که 
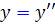. اين همان معادله ديفرانسيل مطلوب است.
ب :
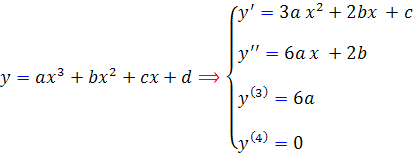
با استفاده از مشتق سوم، مقدار a را بر حسب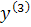 
به دست مي آوريم و با جايگذاري آن در معادله ي مشتق دوم، مقدار b را و پس از آن با جايگذاري اين دو مقدار در معادله ي مشتق، مقدار c را محاسبه مي کنيم. به اين ترتيب مقادير زير را براي a و b و c خواهيم داشت :
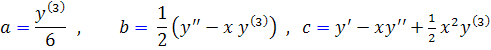
ثابت d هر مقدار دلخواهي مي تواند اختيار کند که ما آن را براي سهولت صفر انتخاب مي کنيم. با جايگذاري مقادير a و b و c در معادله ي y ، معادله ديفرانسيل اين منحني به دست مي آيد :
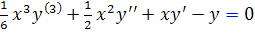
پ :
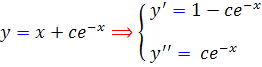
با توجه به معادله ي مشتق دوم و معادله ي y ، معادله ديفرانسيل اين دسته منحني به صورت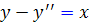 
خواهد بود.
2. الف : براي حل اين معادله از تغيير متغير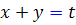 
استفاده مي کنيم. به اين ترتيب خواهيم داشت :
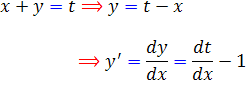
اکنون با جايگذاري تغيير متغير در معادله اصلي به معادله زير مي رسيم :
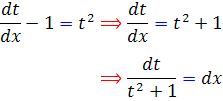
معادله اخير يک معادله ي جداپذير است و جواب عمومي آن به صورت زير است :
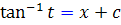
اکنون با برگرداندن تغيير متغير به شکل اصلي جواب عمومي پي خواهيم برد :
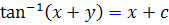
ب : براي حل اين معادله ، تغيير متغير 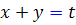را به کار مي بريم . به اين ترتيب رابطه ي زير بين مشتق y و مشتق t برقرار خواهد شد :
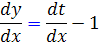
اين تغيير متغير را در معادله اصلي اعمال مي کنيم :
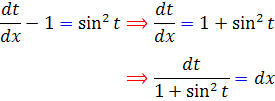
اين معادله نيز يک معادله ي جداپذير است که پس از محاسبه انتگرال هاي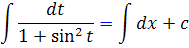 
، - با استفاده از روش هاي انتگرال گيري که در رياضي عمومي مي آموزيم و با استفاده از فرمول هاي مثلثاتي 
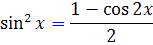و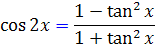 
و با استفاده از تغيير متغير هاي مناسب- به معادله زير دست خواهيم يافت :
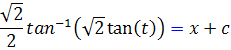
بنابراين جواب معادله ديفرانسيل داده شده به صورت زير خواهد بود :
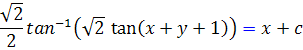
پ :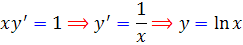 
ت : طرفين اين معادله را بر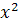 
تقسيم مي کنيم :
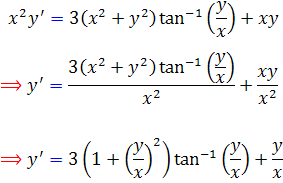
معادله ي اخير ما را به انتخاب تغيير متغير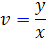 
راهنمايي مي کند. با اين انتخاب خواهيم داشت :
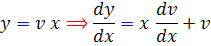
با جانشيني اين متغيرها داريم :
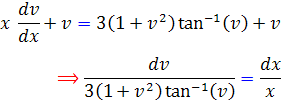
اين معادله نيز يک معادله ديفرانسيل جداپذير است و جواب عمومي آن با محاسبه ي انتگرال هاي
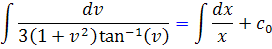
، به صورت زير به دست مي آيد:
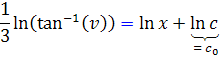
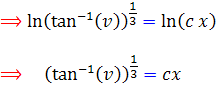
که با جايگزيني تغيير متغير ، شکل صحيح جواب معادله ، اين گونه خواهد بود :
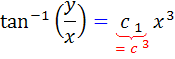
ث :حل اين گونه معادلات را در قسمت معادلات همگن شدني مورد بررسي قرار داديم ، مطابق آن عمل مي کنيم .
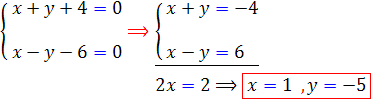
اکنون تغيير متغيرهاي زير را انتخاب مي کنيم :
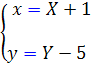
بنابر اين
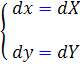
با قرار دادن متغير هاي جديد در معادله اصلي داريم :
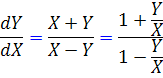
اکنون اگر قرار دهيم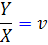 
، آنگاه 
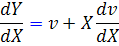. بنابراين
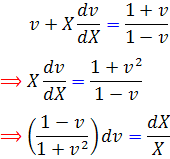
معادله اخير يک معادله جداپذير استاندارد است . با انتگرال گيري داريم :
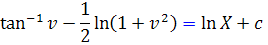
اکنون متغيرها را برمي گردانيم :
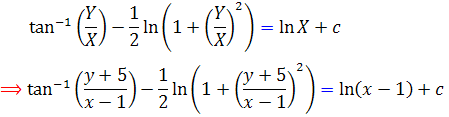
ج : براي حل اين معادله به ترتيب زير پيش مي رويم :
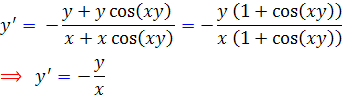
باز هم تغيير متغير 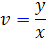را انتخاب مي کنيم . خواهيم داشت :
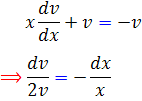
بنابراين با انتگرال گيري داريم :
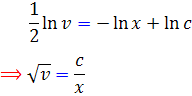
که با برگرداندان تغيير متغير به صورت زير تبديل مي شود :
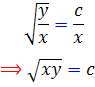
اميدواريم اين پاسخ ها مورد رضايت شما عزيزان قرار گيرد.
