1386/9/26 Midterm Geometry of manifolds Dr. H.Ghane
Geometry of manifolds
Midterm MSc. Exam
Department of MathematicsFerdowsiUniversity of Mashhad
1386/9/26
Dr. H.Ghane’
1. Let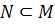 
be a regular submanifold of M. show that 
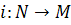( inclusion map ) is an imbedding.
2. If H is a regular submanifold and subgroup of a Lie group G , then H is closed as asubset of G.
3. Show that real projective space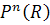 
is a 
.
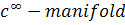4. Let M and N be two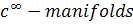 
with dimension m and n respectively with 
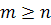. let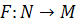 
be a 1-1 immersion . show that F is an open mapping .
5. Show that 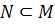is an n-dimentional submanifold of 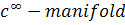M with dimension n if and only if it is an open submanifold ofM.
6. Let G be a Lie grup and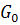 
denote the connected component of G containing the identity element e. show that 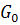is the only connected open subgroup of G.
7. Show that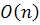 
acts transitively on 
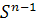and determine the isotropy subgroup of 
.
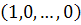