میانترم مبانی ریاضیات محسن پرویزی 14/9/1381 فردسی مشهد
رای دهی: 5 / 5
به نام خدا
اللهم صل علی محمد و آل محمد
نام آزمون : ميانترم مباني رياضيات
نام استاد : محسن پرويزي
تاريخ برگزاري : 14/9/1381
دانشگاه : فردوسي مشهد
دانشكده : علوم رياضي
رشته : رياضي
1. فرض کنيد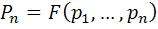 
يک گزاره ي مرکب شامل حداکثر n گزاره 
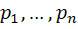باشد، يک تابع ارزش براي 
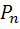به صورت زير تعريف مي شود : 
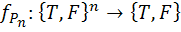و براي هر n-تايي 
، 
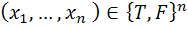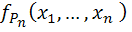دقيقا ً ارزش گزاره ي 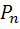است زماني که ارزش 
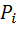را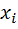 
قرار داده باشيم :
الف : تعداد توابع ارزش را بيابيد.
ب : ثابت کنيد هر تابع دلخواه به صورت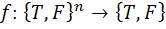 
تابع ارزش يک گزاره ي مرکب مي باشد.
2. اگر A و B دو مجموعه ي متناهي به ترتيب با n و m عنصر باشند :
الف : يک تابع يک به يک 
موجود است اگر و تنها اگر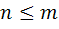 
.
ب : يک تابع پوشا موجود است اگر و تنها اگر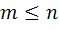 
.
3. فرض کنيد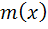 
معرف گزاره ي « x مذکر است » و 
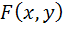معرف « x فرزند y است » باشند. گزاره ي زير را با نماد هاي رياضي بنويسيد، ارزش آن را مشخص کنيد و نقيض آن را بنويسيد.
« کسي هست که خواهر ِ برادر خود نيست »
4. ثابت کنيد اگرA و B دو زير مجموعه ي دلخواه از يک مجموعه مثل X باشند :
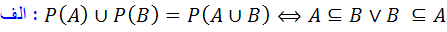
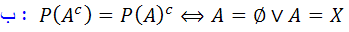
5. فرض کنيد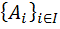 
يک خانواده از مجموعه ها و A مجموعه اي دلخواه باشد :
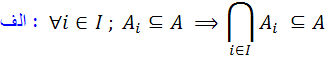
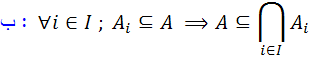
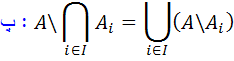
6. فرض کنيد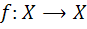 
يک تابع باشد، رابطه ي هم ارزي 
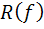را روي X به صورت 
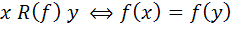تعريف مي کنيم. ثابت کنيد f يک به يک است اگر و تنها اگر 
.
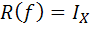7. فرض کنيد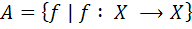 
. روي A رابطه ي R را به صورت زير تعريف مي کنيم : 
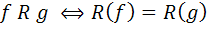که 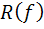همان رابطه ي سؤال 6 است.
الف : ثابت کنيد R يک رابطه ي هم ارزي است.
ب : کلاس هاي هم ارزي تابع ثابت و تابع هماني را بيابيد.
8. در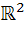 
رابطه ي ~ را به صورت 
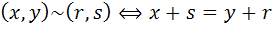تعريف مي کنيم. ثابت کنيد ~ يک رابطه ي هم ارزي است و کلاس هاي آن را به طريق هندسي نشان دهيد.
9. فرض کنيد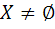 
يک مجموعه و 
. 
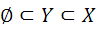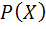را همراه با عمل 
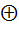( تفاضل متقارن ) در نظر بگيريد.
الف : اگر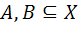 
به قسمي باشند 
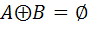آنگاه A=B .
ب : روي 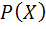رابطه ي o را به صورت زيرتعريف مي کنيم : 
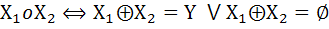. نشان دهيد o يک رابطه ي هم ارزي است که در آن 
.
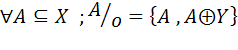10. مشخص کنيد که توابع معرفي شده در زير کداميک ازخواص يک به يک بودن و پوشا بودن را دارا هستند.
الف : هر عدد گويا را مي توان به صورت 
نوشت که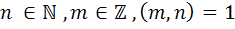 
تابع 
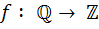را با ضابطه 
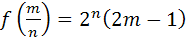در نظر بگيريد.
ب :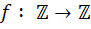 
، 
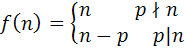که p يک عدد اول ِ ثابت است.
پ : مي دانيم هر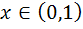
را مي توان به صورت نامتناهي 
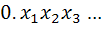نوشت که هر 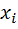يک رقم مي باشد. به عنوان مثال
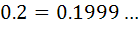. تابع 
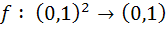را با ضابطه ي 
در نظر بگيريد.
11. فرض کنيد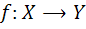 
يک تابع باشد که براي آن توابع 
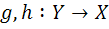موجود باشند که 
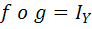و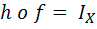 
. ثابت کنيد f وارون پذير است و 
.
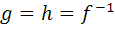12. اگر 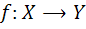يک تابع باشد . دو تابع 
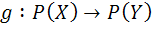و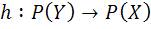 
را با ضابطه ي 
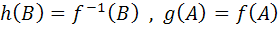تعريف مي کنيم. کدام يک از خواص f را g و h دارا هستند.
