ضابطه تابع، دامنه هم‌دامنه و برد تابع، اختلاف بین هم‌دامنه و برد تابع
- مقطع تحصیلی: عمومی
رای دهی: 4 / 5
تا کنون اطلاعات مقدماتی در مورد تابع و تعریف آن را در سایت ریاضیات ایران آموختیم. اکنون می توانیم وارد مباحث پیشرفته تر در دنیای توابع شویم. اولین قدیم آشنایی با ضابطه تابع، دامنه و برد آن می باشد. با ما همراه باشید...
ضابطه تابع:
به طور کلی ضابطه (فرمول) یک تابع را به صورت زیر نشان می‌دهیم:
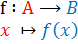
عبارت بالا را این‌گونه می‌خوانیم:
« f تابعی است از مجموعه A به توی مجموعه B به طوری که هر x از A را به مقدار نظیرش یعنی 
از B می‌نگارد.»
مثال1: تابع زیر را در نظر بگیرید:
\( f: \mathbb{R} \rightarrow \mathbb{R}^+ \cup \{0\} \)
\( x \mapsto x^2 \)
این تابع، یک تابع از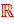 
به توی \(\mathbb{R}^+ \cup \{0\} \) است که هر x را به نظیرش 
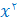می‌نگارد. مثلاً این تابع عدد ۲ به عدد 
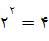تبدیل می‌کند (می‌نگارد).
این تابع همان تابع معروف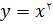 
است.
دامنه، هم‌دامنه و برد تابع:
به مجموعه A در تعریف تابع، دامنه تابع و به مجموعه B ، هم‌دامنه تابع ، و به مجموعه‌ی خروجی های واقعی تابع f، برد تابع می‌گوییم. دامنه تابع مجموعه‌ای است که تابع روی آن تعریف می‌شود و هم‌دامنه‌ی تابع مجموعه‌ای است که خروجی‌های تابع در آن قرار دارد و برد، مجموعه‌ی تمام خروجی‌های واقعی تابع است.
مثال2: در مثال 1 اگر \(\mathbb{R}^+ \cup \{0\} \) را به 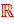تبدیل کنیم، یعنی f تابعی باشد از 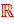به :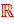
\( f: \mathbb{R} \rightarrow \mathbb{R} \)
دامنه این تابع برابر با 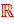، هم‌دامنه تابع نیز برابر با 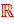ولی برد تابع برابر با \(\mathbb{R^+} \cup \{0\} \) است.
توجه نمایید که در برخی از سؤال‌ها، دامنه تابع داده می‌شود ولی در بسیاری از مسائل دامنه تابع داده نمی‌شود. در این‌گونه موارد دامنه تابع را باید از روی مسأله داده شده یا ضابطه تابع (یا همان فرمول تابع) تشخیص دهیم. مثال زیر را ببینید:
مثال3: سیمی به طول ۴ متر داریم که می‌خواهیم آن را به دو بخش تبدیل کنیم به طوری که هر قطعه تشکیل یک مربع دهد. سیم را از کجا برش دهیم تا دو مربع با هم :
الف- کمترین مساحت را داشته باشند.
ب- بیشترین مساحت را داشته باشند.
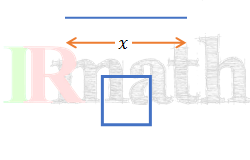
طول ضلع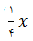 
متر
طول ضلع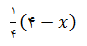 
متر
حل: فرض کنیم قطعه‌ها به ترتیب دارای x و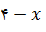 
متر باشند. مساحت هر قطعه مانند شکل، به ترتیب 
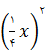و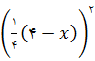 
متر مربع می‌باشد. بنابراین مساحت کل ، yمتر مربع، عبارت است از:
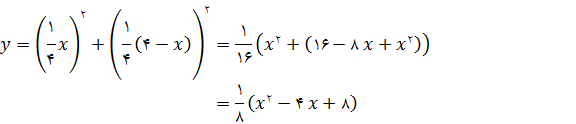
توجه کنید که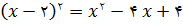 
پس y را می‌توانیم به صورت زیر بنویسیم:
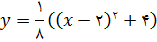
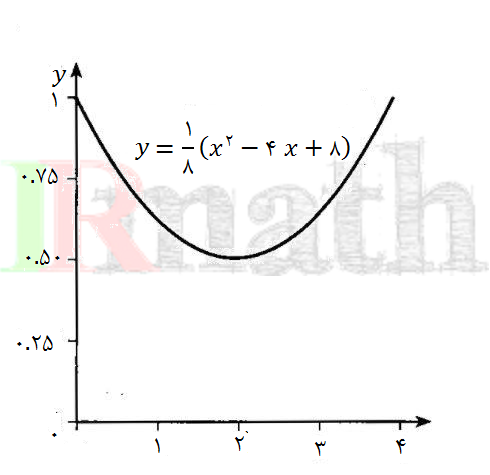
نمودار تابع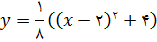
حالا مقدار این عبارت را می‌توانیم به ازای هر عدد حقیقی x بدست آوریم، اما از مسأله پیداست که فقط xهای بین صفر تا چهار را می‌خواهیم. نمودار این تابع در بازه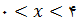 
را ببینید. چون همیشه 
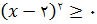، پس کمترین مساحت وقتی به دست می‌آید که 
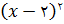صفر شود. یعنی 
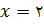. پس کمترین مساحت ۰٫۵ متر مربع می‌شود.
از روی نمودار دیده می‌شود که بیشترین مساحت برابر با یک متر مربع است و این زمانی اتفاق می‌افتد که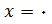
یا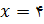 
. اما این مقادیر xغیرقابل قبول است زیرا با این مقادیر نمی‌توان سیم را به دو قطعه تقسیم کرد. ما می‌توانیم به بیشترین مساحت یعنی یک متر مربع، هر چقدر که بخواهیم نزدیک شویم، اما نمی‌توانیم دقیقاً به آن برسیم. بنابراین بیشترین مساحت وجود ندارد.
در درس های بعدی سایت ریاضیات ایران در مورد نمودار توابع، انواع تابع و خواص توابع بحث خواهیم کرد. لطفا نظرات و انتقادات خود و اشکالات و نواقص ما را در انتهای همین صفحه ثبت نمایید.
