Finite Groups , 27 November 2007, A. Erfanian
رای دهی: 3 / 5
Finite Groups
Midterm MSc. Exam
Department of MathematicsFerdowsiUniversity of Mashhad
27 November 2007
A. Erfanian
1. a. Define k-transitive and k-homogenous group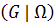 
.
b. Prove that if G is transitive and for every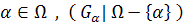 
is (k-1)-transitive, then G is k-transitive.
c. Give an example of a Double transitive groups.
2. a. Define a non-trivial block and give an example.
b. Prove that if 
and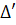 
are two blocks of 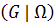, then 
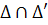is also a block of G.
c. is it true the union of two blocks are always a block?
3. a. Define a primitive and imprimitive group and give an example for each.
b. Let 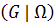be a transitive group. Then prove that if for every 
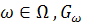is a maximal subgroup of G, then 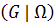is primitive.
4. a. Define a transvection and prove that if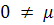 
is a linear functional and 
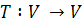is a linear transformation by the rule 
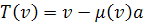is a transvection on a suitable hyperplan H and 
.
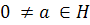b. Prove that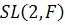 
can be generated by transvections.
c. Compute the order of groups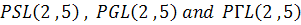 
.
