5.2. بخش پذیری بر اعداد اول ( بخش پذيري بر عدد 7 )
چه اعدادی بر 7 بخش پذیرند ؟ چه اعدادی بر 13 بخش پذیرند ؟ چه اعدادی بر 17 بخش پذیرند ؟ امروزه با استفاده از ماشین حساب ها ، دانستن قوانین بخش پذیری بر اعداد ، کمتر احساس نیاز می شود . اما یاد گیری این قوانین می تواند افق جدیدی را درباره ی ویژگی های اعداد طبیعی پیش روی ما باز کند .
با احتمال زیاد ، شما قوانین بخش پذیری بر اعداد اول را نمی دانید . در ادامه ما تعدادی از از این قوانین را بین می کنیم که روشی دیگر برای یافتن قوانین را به شما آموزش می دهد .
قانون بخش پذیری بر 7 :
... « رقم یکان را حذف کنید و دو برابر آن را از عدد ِ جدید کم کنید. اگر عدد باقی مانده بر 7 بخشپذیر باشد، آنگاه عدد اصلی نیز بر 7 بخش پذیر است. در صورتی که عدد انتخابی بزرگ باشد، این روند را برای عدد باقی مانده ، آنقدر تکرار کنید تا تشخیص بخش پذیری ِ آن بر 7 برای شما ممکن باشد. » ...
به مثال زیر توجه کنید :
مثال 1.2 : آیا عدد 256742 بر 7 بخش پذیر است ؟
حل : این عدد را در نظر بگیرید. رقم یکان آن 2 است. آن را حذف می کنیم. عدد جدید ِ 25674 به دست می آید. اکنون دو برابر رقمی را که حذف کرده ایم ؛ یعنی ![]() ؛ را از عدد جدید کم می کنیم :
؛ را از عدد جدید کم می کنیم :
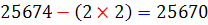
اگر این عدد بر 7 بخش پذیر باشد آنگاه عدد 256742 نیز بر 7 بخش پذیر است اما هنوز نمی توانیم تشخیص دهیم آیا 25670 بر 7 بخش پذیر است یا خیر ؟بنابراین قانون را برای 25670 تکرار می کنیم :

اگر 2567 بر 7 بخش پذیر باشد، عدد 25670 بر 7 بخش پذیر خواهد بود و در نتیجه عدد 256742 نیز بر 7 بخش پذیر خواهد بود. آیا می توانید تشخیص دهید 2567 بر 7 بخش پذیر است یا خیر ؟ اگر نمی دانید قانون را تکرار کنید :
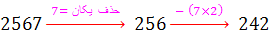
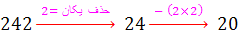
چون عدد 20 بر 7 بخشپذیر نیست ، عدد اصلی و اعداد 25670 و 2567 و 242 نیز بر 7 بخش پذیر نیستند. ( امتحان کنید !!!! )
مثال 2.2 : آیا عدد 876547 بر 7 بخش پذیر است ؟
حل : قانون بخش پذیری بر 7 را برای این عدد اعمال می کنیم :
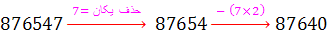

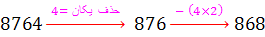
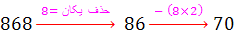
در این مرحله واضح است که 70 بر 7بخش پذیر است. بنابراین اعداد ِ 868 و 8764 و 87640 و 876547 همگی بر 7 بخش پذیرند. ( امتحان کنید !!! )
برای آنکه شما بیشتر با این قانون آشنا شوید، بهتر است با جند عدد اننتخابی این قانون را بیشتر تجربه کنید و نتیجه را با آنچه ماشین حساب می گوید، مقایسه کنید. این قانون را بیاموزید چرا که قوانین بخش پذیری بر دیگر اعداد اول نیز روندی مشابه به این قانون دارند.
آیا می دانید این فرمول از کجا آمده است ؟
در جدول زیر تمامی اعدادی را مشاهده می کنید که می توانند در رقم یکان جای بگیرند. در هر یک از حالت ها ، مشخص شده است هنگامی که رقم یکان حذف می شود و دو برابر آن از عدد جدید کسر می شود، چه اتفاقی می افتد. در این صورت گویی از عدد اصلی مضربی از 7 کسر می شود. با ادامه ی این روند ، اگر ععد باقی مانده بر 7 بخش پذیر باشد، عدد اصلی نیز بر 7 بخش پذیر است. در واقا با این روند، عدد اصلی به دو قسمت تبدیل می شود که هر کدام از آنها بر 7 بخش پذیرند.
| رقم پایانی ( رقم یکان ) | عدد کم شده از عدد اصلی |
| 1 | 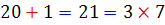 |
| 2 | 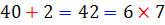 |
| 3 | 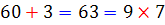 |
| 4 | 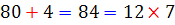 |
| 5 | 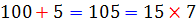 |
| 6 | 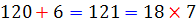 |
| 7 | 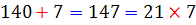 |
| 8 | 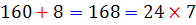 |
| 9 | 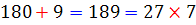 |
















