تابع ثابت، تعریف، فرمول، نکات، مثال و تمرین
رای دهی: 5 / 5
تابع ثابت
اکنون که با مفهوم تابع و نمودار تابع آشنا شدید، به معرفی توابع می‌پردازیم. در این درس در مورد تابع ثابت صحبت خواهیم کرد، ضابطه آن را خواهیم دید ، نمودار آن را رسم می‌کنیم و چند مثال خواهیم داشت.
آیا تا کنون ضرب المثل «حرف مرد یکی است» را شنیده‌اید؟ همیشه حرفش یکی است! یعنی هرچه شما بگویید، او فقط یک حرف می زند! تابع ثابت نیز چنین است! ببینید:
تعریف تابع ثابت:
تابع 
را یک تابع ثابت می‌گوییم هرگاه به ازای هر ورودی x از دامنه ، خروجی مقدار ثابتی (عددی) مانند c باشد یعنی برای هر x داشته باشیم 
.
به طور کلی تابع ثابت به صورت زیر تعریف می‌شود:
بخوانید: f تابعی از 
به که هر x را به عدد ثابت c می‌نگارد.
مثال: تابع 
یک تابع ثابت است زیرا شما هر مقداری که برای x انتخاب کنید، خروجی عدد ثابت ۳ خواهد بود. جدول زیر را ببینید:
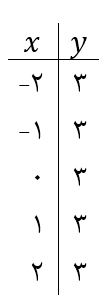
حال نمودار این تابع را رسم می کنیم. ابتدا نقاط جدول بالا را روی دستگاه پیدا می کنیم:
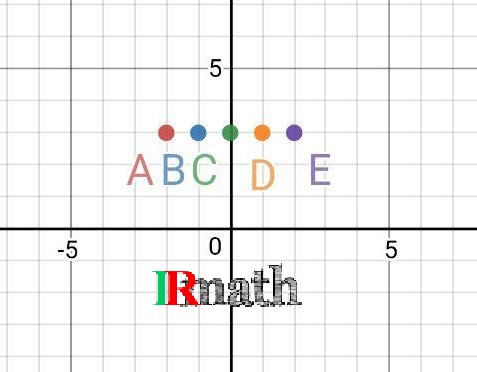
و سپس این نقاط را با توجه به ضابطه تابع، به هم وصل می کنیم و از دو طرف ادامه می دهیم، شکل زیر بوجود می‌آید:
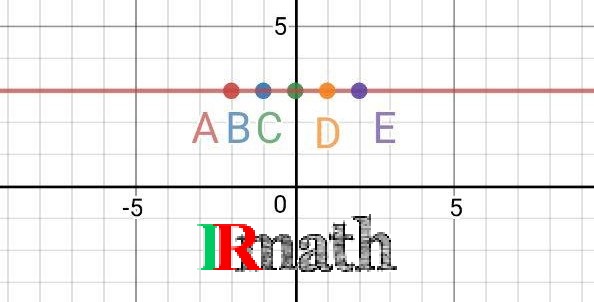
همان طور که در شکل بالا می‌بینید، نمودار تابع ثابت، یک خط افقی است که به موازات محور x ها امتداد می‌یابد. دامنه تابع ثابت، مجموعه اعداد حقیقی یعنی می‌باشد مگر اینکه اطلاعات مسأله، دامنه آن را محدود کند. برد تابع ثابت فقط شامل یک عدد است. بنابراین در جایی که ابهامی وجود نداشته باشد، از ذکر دامنه و برد تابع ثابت خودداری می‌کنیم و فقط می‌نویسیم 
.
تمرین: تابع‌های زیر را رسم کنید:
الف: 
ب: 
ج: 
وقتی 
باشد و 
وقتی x<2 باشد.
د: وقتی 
باشد و 
وقتی 
باشد و 
وقتی 
باشد.
هـ: 
وقتی باشد و 
وقتی 
باشد.
نمودار قسمت هـ را با هم رسم کنیم. سایر قسمت‌ها را خودتان رسم کنید.
همان طور که مسأله بیان کرده است، عمل می‌کنیم: ابتدا قسمتی که باشد را رسم می‌کنیم. نمودار به صورت شکل زیر خواهد بود.
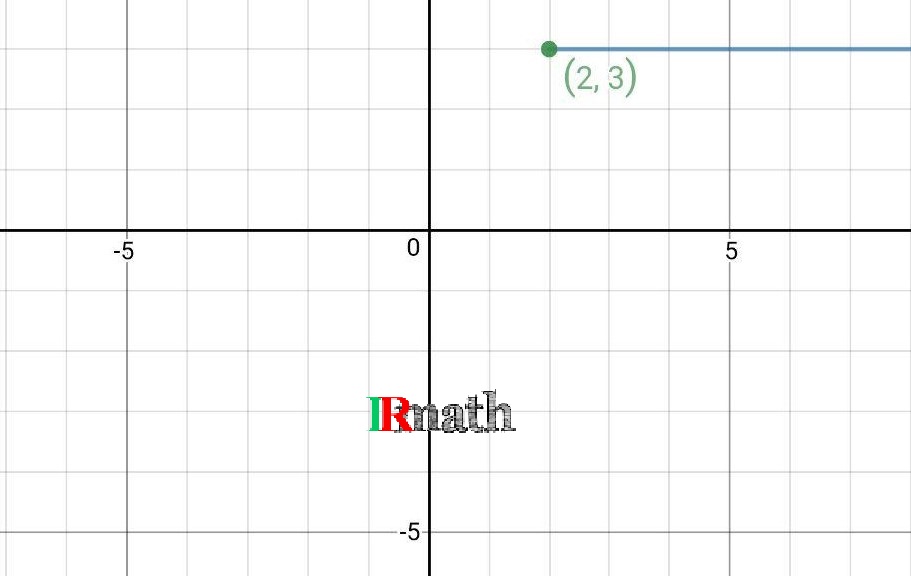
دقت کنید برای تأکید بر اینکه 
در عبارت در دامنه تابع وجود دارد، این نقطه را روی نمودار با دایره‌ای توپر نشان داده‌ایم. این یک رسم خیلی خوب در ریاضیات است. همچنین اگر بخواهیم تأکید کنیم که نقطه‌ای از دامنه روی نمودار نیست، آن نقطه را با دایره‌ای توخالی مشخص می‌کنیم. اکنون نمودار قسمت دوم تابع را نیز به صورت زیر می‌افزاییم:
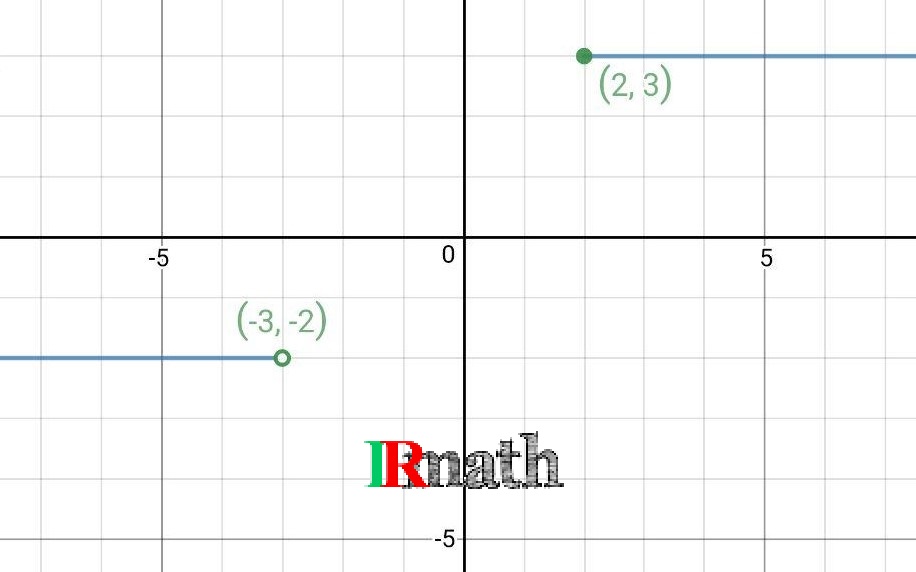
دقت کنید که در اینجا نیز نقطه نظیر 
را با توجه به عبارت به صورت دایره‌ای توخالی نشان دادیم.
سؤال. اگر برد تابع ثابت 
به صورت 
باشد، حاصل 
کدام است؟
الف- 1
ب- 2
ج- 3
د- 5
حل: در این سؤال باید مقدار را به دست آوریم. چون مسأله گفته تابع ثابت است، پس برد آن باید مجموعه‌ای تک عضوی باشد، یعنی با توجه به مجموعه برد باید داشته باشیم :
اکنون با انتقال ضرایب مجهول به یک سمت مساوی داریم:
پس
پس
.♦
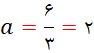
در جلسات بعدی با توابع پیچیده تری آشنا خواهیم شد. هرچه جلوتر رویم، مباحث کامل تر خواهد شد. با ریاضیات ایران همراه باشید.
