پایانترم آنالیز ریاضی3،فردوسی مشهد،ربیعی،خرداد 85
رای دهی: 5 / 5
به نام خدا
اللهم صل علی محمد و آل محمد
نام آزمون : پايان ترم آناليز رياضي 3
نام استاد : دکتر ربيعي
تاريخ برگزاري : خرداد ماه 85
دانشگاه : فردوسي مشهد
دانشكده : علوم رياضي و آمار
1. صورت قضيه ي تابع معکوس را بيان کنيد ( اثبات لازم نيست ) و با استفاده از آن نشان دهيد اگر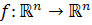 
يک نگاشت 
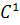باشد که در هر 
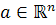داشته باشيم 
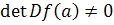آنگاه f يک نگاشت باز است.
2. صورت قضيه ي تابع ضمني را بيان کنيد ( اثبات لازم نيست ) و با استفاده از آن نشان دهيد که معادله ي زير داراي بينهايت جواب است.
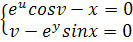
3. فرض کنيد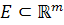 
يک زيرمجموعه ي باز و 
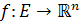يک تابع 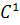باشد. منظور از مشتق دوم f در نقطه ي 
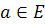را بيان کنيد و سپس قضيه ي مقابل را اثبات کنيد : اگر 
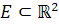باز و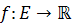 
به صورتي باشد که 
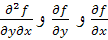در هر نقطه ي E موجود باشند. آنگاه اگر 
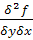در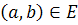 
پيوسته باشد آنگاه 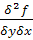در 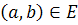وجود دارد و بعلاوه در 
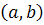داريم :
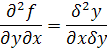
4. اگر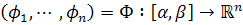 
يک راه از 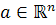به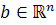 
باشد منظور از طول پذير بودن اين راه را بيان کنيد و سپس قضيه ي مقابل را ثابت کنيد : نشان دهيد راه 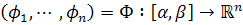طول پذير است اگر و تنها اگر توابع 
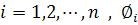، توابع با تغيير کراندار باشند.
5. منظور از محتواي صفر را براي زيرمجموعه هاي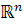 
بيان کنيد و نشان دهيد اگر 
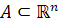کراندار و 
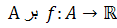انتگرال پذير باشد آنگاه مرز A مجموعه اي با محتواي صفر است.
به يک سوال از دو سوال زير به دلخواه پاسخ دهيد.
6. فرض کنيد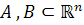 
زيرمجموعه ي باز کرانداري باشند که 
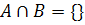و فرض کنيد 
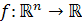تابعي کراندار باشد. نشان دهيد اگر f بر A و B انتگرال پذير باشد آنگاه f بر 
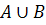نيز انتگرال پذير است و داريم :
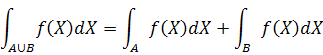
7. منظور از يک immersion و يک imbedding را بيان کنيد و نشان دهيد که ترکيب هر دو immersion نيز يک immersion است.
