امتحان میان ترم جبر 2 دکتر چیتی 30/2/1385 فردوسی مشهد
رای دهی: 5 / 5
نام آزمون : میان ترم جبر 2
نام استاد : دکتر چیتی
تاریخ برگزاری : 30/2/1385
دانشگاه : فردوسی مشهد
دانشکده : علوم ریاضی
۱. آ : یک خود ریختی داخلی گروه G را تعریف کنید.
ب : اگر G گروه و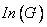 
خودریختی های داخلی آن باشد، ثابت کنید :
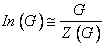
پ : اگر گروه خودریختی های G یعنی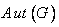 
یک گروه دوری باشد ثابت کنید G آبلی است.
۲. آ : اگر G گروه و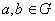 
آنگاه جابحاگر a و b را تعریف کنید.
ب : اگر G گروه و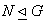 
آنگاه ثابت کنید 
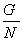آبلی است اگر و فقط اگر 
.
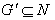۳. آ : یک سری ترکیب برای گروه G را تعریف کنید.
ب : قضیه ی جردن-هلدر را بیان و اثبات کنید.
پ : تمام سری های ترکیب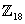 
را بنویسید و نشان دهید که با هم معادل اند.
۴. آ : گروه پوچ توان را تعریف نمایید.
ب : ثابت کنید هر زیر گروه یک گروه حل پذیر خود گروهی است حل پذیر.
پ : ثابت کنید گروه غیر بدیهی G ساده و حل پذیر است اگر و فقط اگر دوری از مرتبه ئ عدد اول باشد.
۵. فرض کنید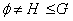 
به طوری که 
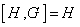ثابت کنید G نمی تواند پوچ توان باشد.
